Stochastic Qwak on a Maze#
Models of Stochastic Quantum Walks on different kinds of
graphs have been used in the literature to model the remarkably efficient
energy transport phenomena in light-harvesting complexes, in
which the external noisy environment plays a fundamental role. Here, we will show how
to run a Stochastic Quantum Walk on a particular kind of graph, the perfect maze,
by using the QWAK package.
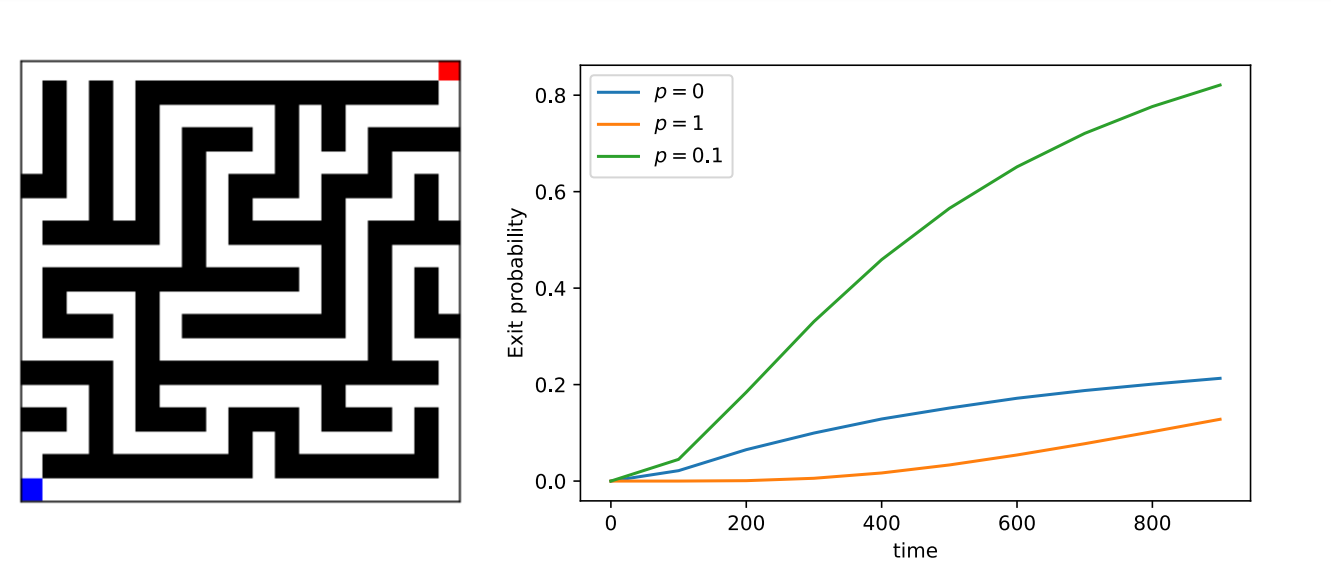
A perfect maze is defined to be a maze with one and only one path connecting
the entrance with the exit. For example, one can observe, in the random maze in
the following figure that there is only one path connecting the maze
entrance (blue node) to the exit (red node). We can generate a random perfect
maze, by looking at earlier works in the literature
that worked with quantum walks on mazes and then just extract their adjacency
matrix in order to define our Stochastic Quantum Walker on QWAK. To
properly define the walker we need to specify some additional parameters with
respect to the CTQW case. First, the noise parameter \(p \in [0,1]\), that
specifies the amount of noise that our SQW has. If a sink node (or exit node)
is present we also need to specify its index \(n\) and the sink rate \(\Gamma\) of
the corresponding Linblad operator. We can thus simply instantiate our SQW
object as follows:
1p = 0.1
2n = 99
3Gamma = 0.99
4
5graph = nx.from_numpy_array(maze_graph.adjacency)
6qwak = StochasticQWAK(graph, noiseParam=p,
7 sinkNode=n, sinkRate=Gamma)
Now that we have instantiated our StochasticQWAK object, we can make it
evolve by the usual runWalk command. For example, we can see that if
we run SQWs with different noise parameters \(p\) and plot the exit probability
from the sink node as a function of time as reported in the previous figure,
we obtain that the \(p=0.1\) walker has a much higher
exit rate than both the purely quantum and purely classical walker (\(p=0\) and
\(p=1\) respectively). This is a result analogous to well-known noise-assisted
transport phenomena on networks that we were able
to reproduce in just a few lines of code with the QWAK package.