Perfect State Transfer#
To showcase the capabilities of the perfect state transfer (PST) functionality within QWAK, we present a hands-on example featuring a quantum walk on a 4-dimensional hypercube graph. This choice of graph is particularly instructive because hypercube graphs are a well-studied class of graphs with interesting topological properties. For this demonstration, we initialize the quantum walk at vertex 0. This choice of initial vertex serves as the starting point for the state transfer process.
1n = 4
2graph = nx.hypercube_graph(n)
3initcond = [0]
4
5qw = QWAK(graph=graph)
6t = eval(str(qw.checkPST(0,15)))
7qw.runWalk(time=t, initStateList=initcond)
8plt.plot(qw.getProbVec())
In the above code, a 4-dimensional hypercube with 16 nodes is created using
NetworkX. The walker starts at vertex 0, and the checkPST
function returns the time value for which PST occurs between the antipodal
vertices, or -1 if it does not. For this hypercube, PST happens at \(t =
\frac{\pi}{2}\), consistent with all N-dimensional hypercubes. This can be confirmed by iteratively
running the checkPST function for all antipodal vertex pairs contained
in the structure. The quantum walk is then executed for this time duration via
runWalk, and Matplotlib is used to plot the resulting
probability vector, showing complete transfer from vertex 0 to 15.
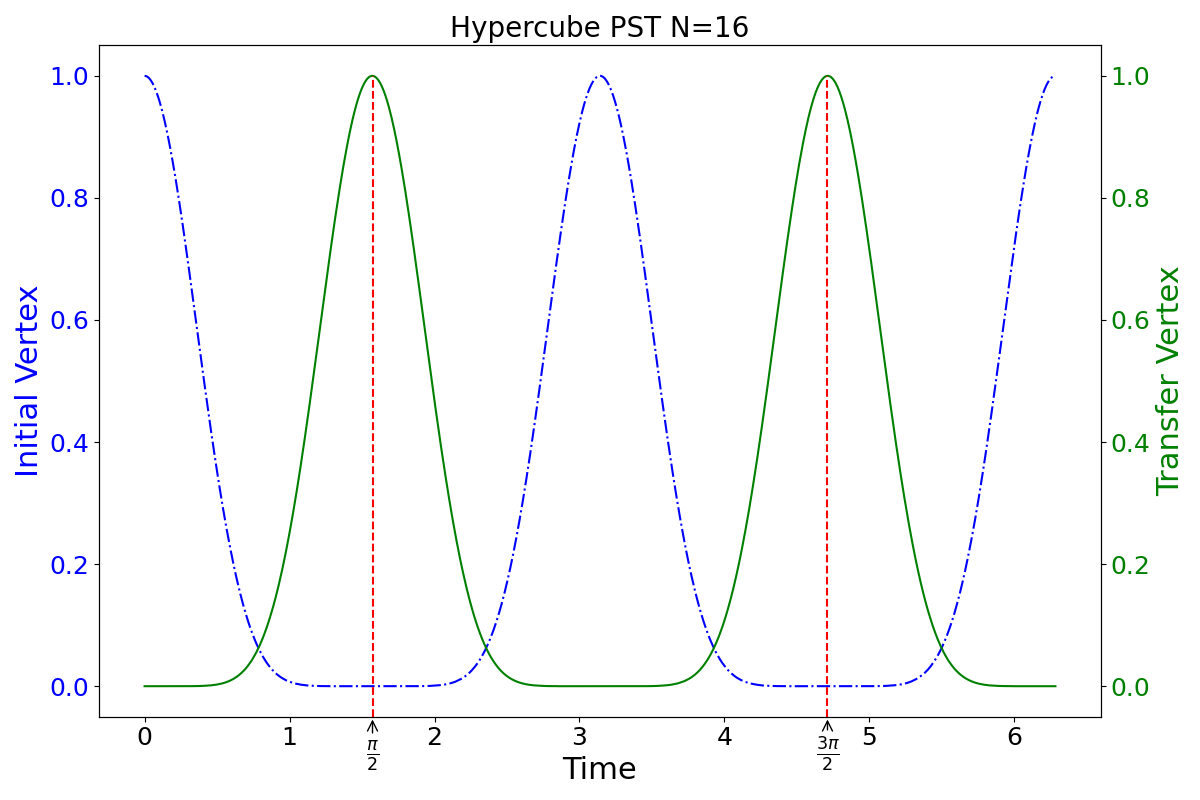
The previous figure was plotted using an utility function present in the notebook, illustrating the evolution of the probability of finding a walker between the vertices we expect PST to occur. PST is a cyclic phenomenon that occurs every \(2\tau\), being \(\tau\) the initial PST time (in this case \(\pi/2\)). This is a direct consequence of the fact that there is PST from vertex \(a\) to \(b\), then there is also from \(b\) to \(a\). This can all be observed in the figure with the blue lines indicating the evolution for the initial vertex and the green line for the final vertex. Notice that PST return to the original vertex every \(t=\pi\), since PST occurred at time \(\pi/2\) from vertex 0 to vertex 15, then at time \(\pi/2 + \pi\) the walker returns to vertex 15. PST is successfully achieved, confirming the efficacy of the algorithm.